A diszkrét valószínűségi változók
Véletlen változó nevű változó értékét, ami annak az eredménye, minden egyes vizsgálat előtt úgy egy ismeretlen érték, ami attól függ, hogy a véletlen okoz. Véletlen változók jelöljük tőke latin betűk: $ X, \ Y \ Z \ \ dots $ típusuk szerint véletlen változók lehetnek diszkrét és folytonos.
Diszkrét valószínűségi változó - ez egy véletlen változó, amelynek értéke nem lehet több, mint a megszámlálható, azaz véges vagy megszámlálható. Kevesebb countability azt jelenti, hogy az értékek a véletlen változó lehet sorolni.
1. példa. Íme néhány példa a diszkrét valószínűségi változók:
a) a találatok száma a cél a $ n $ felvételek lehetséges értékeit $ 0, \ 1, \ \ dots, \ n $.
b) a számát címerek a lehullott pénzfeldobást, ahol a lehetséges értékeit $ 0, \ 1, \ \ pontok, \ n $.
c) az érkezők száma hajó fedélzetén (megszámlálható értékrend).
g) a hívások számát jön a PBX (megszámlálható értékrend).
1. Jog diszkrét valószínűségi eloszlás valószínűségi változó.
Egy diszkrét véletlen változó $ X $ vehet az értékeket $ x_1, \ dots \ x_n $ valószínűséggel $ p \ left (x_1 \ right) \ \ dots \ o \ left (x_n \ right) $. A megegyezést ezeket az értékeket és azok valószínűségét nevezzük a törvény a diszkrét véletlen változó. Általános szabály, hogy az ilyen leveleket kap az asztalnál az első sorban, amelyek jelzik az értékeket $ x_1, \ dots \ x_n $, és a második sor ezeknek megfelelő értékek valószínűségi $ p_1, \ dots \ p_n $.
$ \ Begin
\ hline
x_i x_1 x_2 \ dots x_n \\
\ hline
p_i p_1 p_2 \ dots p_n \\
\ hline
\ End $
2. példa. Hagyja, hogy a véletlen változó $ X $ - száma csökkent pontot a dobás a kockával. Az ilyen véletlen változó $ X $ vehet a következő értékeket $ 1 \ 2 \ 3 \ 4 \ 5 \ 6 $. Annak a valószínűsége, ezek az értékek egyenlő 1 $ / 6 $. Ezután a törvény eloszlása véletlenszerű változó $ X $:
$ \ Begin
\ hline
1 2 3 4 5 6 \\
\ hline
1/6 1/6 1/6 1/6 1/6 1/6 \\
\ hline
\ End $
2. Az elvárás egy diszkrét véletlen változó.
Az elvárás a véletlen mennyiség határozza meg „center” értéket. Diszkrét véletlen változó elvárás összegeként kiszámított értékek $ x_1, \ dots \ x_n $ ezeknek megfelelő értékek valószínűségi $ p_1, \ dots \ p_n $, azaz: $ M \ left (X \ right) = \ sum ^ N_ $. Az angol nyelvű irodalom egy másik jelölést $ E \ left (X \ right) $.Tulajdonságai a várakozás $ M \ left (X \ right) $:
- $ M \ left (X \ right) $ között van a legkisebb és legnagyobb értékei valószínűségi változó $ X $.
- Elvárás a legállandóbb állandó, azaz, $ M \ left (C \ right) = C $.
- A konstans tényező lehet venni, mint egy jel a matematikai elvárás: $ M \ left (CX \ right) = CM \ left (X \ right) $.
- A matematikai elvárás összege véletlen változók összegével egyenlő a matematikai elvárások: $ M \ left (X + Y \ right) = M \ left (X \ right) + M \ left (Y \ right) $.
- A matematikai elvárás a termék független valószínűségi változók egyenlő a termék a matematikai elvárások: $ M \ left (XY \ right) = M \ left (X \ right) M \ left (Y \ right) $.
3. példa. Mi található a várakozás egy véletlen változó $ X $ példában $ 2 $.
Megfigyelhető, hogy a $ M \ left (X \ right) $ között fekszik a legalacsonyabb ($ 1 $), és a legnagyobb ($ 6 $) értékei valószínűségi változó $ X $.
4. példa. Köztudott, hogy a matematikai elvárás egy véletlen változó értéke $ X $ $ M \ left (X \ right) = $ 2. Keresse meg a várakozás egy véletlen változó $ 3X + $ 5.
A fenti tulajdonságok, kap $ M \ left (3X + 5 \ right) = M \ left (3X \ jobb) + M \ left (5 \ right) = 3M \ left (X \ jobb) + 5 = 3 \ cdot 2 + 5 = 11 $.
5. példa. Köztudott, hogy a matematikai elvárás egy véletlen változó értéke $ X $ $ M \ left (X \ right) = 4 $. Keresse meg a várakozás egy véletlen változó $ 2X-9 $.
A fenti tulajdonságok, kap $ M \ left (2X-9 \ right) = M \ left (2X \ right) -M \ left (9 \ right) = 2 M \ left (X \ right) -9 = 2 \ cdot 4 -9 = -1 $.
3. A diszperziós diszkrét véletlen változó.
Lehetséges értékek valószínűségi változók egyeznie az átlagos változó lehet szétszórva az átlagértékeket. Például, a két hallgatói csoport, az átlagos pontszám a vizsgát az elmélet a valószínűség egyenlő volt 4, de az egyik csoport volt minden horoshist, és a másik csoport - csak troechniki és kitüntetéssel. Ezért szükség van az ilyen számszerű jellemzőinek valószínűségi változók, amelyek terjedését mutatják értékeit véletlen változó a várakozás. Egy ilyen jellemző variancia.
A változás egy diszkrét véletlen változó $ X $ jelentése:
Az angol nyelvű szakirodalom felhasználásával jelölést $ V \ left (X \ right) \ Var \ left (X \ right) $. Nagyon gyakran, a diszperzió $ D \ bal (X \ right) $ képlettel számítottuk ki $ D \ bal (X \ right) = \ sum ^ n _- ^ 2 $.diszperziós tulajdonságait $ D \ left (X \ right) $:
- A változás mindig nagyobb vagy egyenlő, mint nulla, azaz $ D \ left (X \ right) \ ge 0 $.
- Diszperziós állandók értéke nulla, azaz a $ D \ left (C \ right) = 0 $.
- Állandó faktor lehet venni, mint a jele, diszperzió, feltéve négyzet azt, azaz a $ D \ left (CX \ right) = C ^ 2D \ left (X \ right) $.
- A változás az összeg független valószínűségi változók egyenlő összegével eltéréseket, azaz $ D \ left (X + Y \ right) = D \ left (X \ jobb) + D \ left (Y \ right) $.
- A változás a különbség független valószínűségi változók egyenlő összegével eltéréseket, azaz $ D \ left (X-Y \ right) = D \ left (X \ jobb) + D \ left (Y \ right) $.
6. példa. Kiszámoljuk a szórás a véletlen változó $ X $ $ példa 2 $.
7. példa. Köztudott, hogy a szórás egy véletlen változó értéke $ X $ $ D \ left (X \ right) = $ 2. Keresse meg a szórás a véletlen változó $ 4X + 1 $.
A fenti tulajdonságok, megtalálja $ D \ bal (4x + 1 \ right) = D \ left (4X \ jobb) + D \ bal (1 \ right) = 4 ^ 2D \ left (X \ jobb) + 0 = 16D \ bal (X \ right) = 16 \ cdot 2 = 32 $.
8. példa. Köztudott, hogy a szórás egy véletlen változó értéke $ X $ $ D \ left (X \ right) = 3 $. Keresse meg a szórás a véletlen változó $ 3-2X $.
A fenti tulajdonságok, megtalálja $ D \ bal (3-2X \ right) = D \ left (3 \ jobb) + D \ left (2X \ right) = 0 + 2 ^ 2D \ left (X \ right) = 4D \ bal (X \ right) = 4 \ cdot 3 = 12 $.
4. Az eloszlásfüggvény egy diszkrét véletlen változó.
Módszer ábrázolása diszkrét véletlen változó eloszlása, mint egy sor nem kizárólagos, és ami a legfontosabb, hogy nem általános, hiszen a folyamatos véletlen érték nem állítható be egy számot forgalmazás. Van egy másik módja a képviselő valószínűségi változó - eloszlásfüggvény.
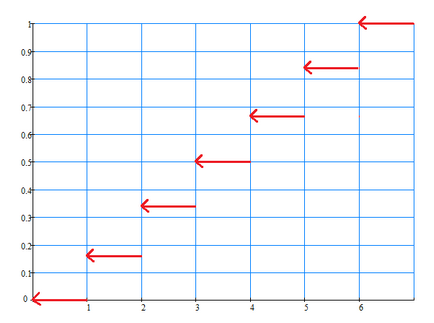
Eloszlásfüggvénye véletlen változó $ X $ függvénye $ F \ left (x \ right) $, ami meghatározza a valószínűsége, hogy egy véletlenszerűen változó $ X $ értéket vesz fel kevesebb, mint egy fix érték $ x $, azaz $ F \ left (x \ right) = P \ left (X A tulajdonságok az eloszlási függvény: 9. példa. Keressük az eloszlásfüggvény $ F \ left (x \ right) $ a törvény eloszlása diszkrét véletlen változó $ X $ példában $ 2 $. $ \ Begin Ha a $ x \ le 1 $, akkor nyilvánvaló, $ F \ left (x \ right) = 0 $ (beleértve a $ x = 1 $ $ F \ left (1 \ right) = P \ left (X <1\right)=0$). Ha a $ 1 Ha a $ 2 Ha a $ 3 Ha a $ 4 Ha a $ 5 Ha a $ x> 6 $, akkor a $ F \ left (x \ right) = P \ left (X = 1 \ jobb) + P \ left (X = 2 \ jobb) + P \ left (X = 3 \ right) + P \ left (X = 4 \ jobb) + P \ left (X = 5 \ jobb) + P \ left (X = 6 \ right) = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1 $. Menetrend eloszlás $ F \ left (x \ right) $:
\ hline
1 2 3 4 5 6 \\
\ hline
1/6 1/6 1/6 1/6 1/6 1/6 \\
\ hline
\ End $